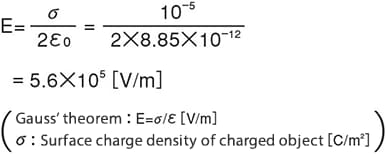Fundamentals of Electric Fields and Force
When an electrical current flows through an object, there is always an electric field. This section covers basic knowledge about what an electric field is and details how to calculate electric fields using Coulomb’s Law.
What is an electric field?
Electric charge is the amount of electricity a charged object has. If an object has more electrons than protons, it is negatively charged. If an object has fewer electrons than protons, it is positively charged. Electric charge is represented by the symbol Q and is measured in a unit called coulombs (C). If the two charges Q1 and Q2 are separated by a distance r [m], then the force working between the charges, represented as F [N], is given by Coulomb’s Law as follows:
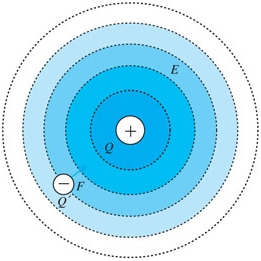
The electric field strength gets weaker as the distance from the charge increases.
An electric field (E-field) exists around a charged object and is the area where there is force acting on that electric charge. For example, a point charge* in space brings special properties to that surrounding space. When a different point charge comes along, the acting force in that space acts on that point charge. This can be understood as the “sphere of influence” of the charge. As shown in the picture, the strength of this influence gets smaller the farther you get from the centre. The magnitude of an electric field is called electric field strength, which expands outward from the centre as shown in the picture and gets weaker as the distance from the charge increases.
Due to the nature of electric fields, this force has directionality, and therefore it is expressed in vector form. An electric field has both magnitude and direction.
Point charge: An electric charge located in an object so tiny that its size is not measurable
A point charge Q [C] in space with an acting force F [N] has an electric field strength as follows:
E=F/Q[V/m]
The electric field unit [V/m] represents the potential difference per unit distance. Rearranging this, you get:
F=QE[N]
This represents Coulomb force, which is the force acting on charges in the electric field.
From the above expression, the electric field strength produced by the point charge can be expressed as follows:
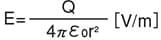
A point charge with an amount of charge Q [C] creates an electric field in the space around it, whose strength is inversely proportional to the square of the distance from the point charge r [m].
Lines of electric force
The direction of electric field is the direction from positive charge toward negative charge.
The lines of electric force are virtual lines depicting the direction of the electric field as shown in the picture below. The direction of the arrows in the lines of electric force shows the electric field. The electric field is directed from positive to negative.
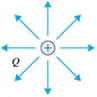
of a positive point charge
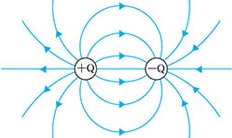
when positive and negative point charges are present
As shown below, the lines of electric force come out vertically from the surface in the case of a charged object (conductor). If the surface charges of this object are distributed with the same density, the lines of electric force will also be arranged at equal intervals. The density represents the size of the potential. A large number of lines of electric force arranged at short intervals indicate a strong electric field while a smaller number of lines of electric force with wider intervals indicate a weaker electric field.
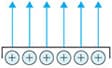
of a charged object (conductor)
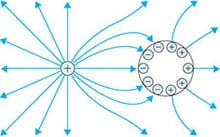
when there is a conductor near the charged object
Gauss’ theorem
When there is a charge in an electric field, you can calculate the electric field based on its amount and shape. Gauss’ theorem is used to calculate electric fields using this approach. Calculating an approaching charged object’s electric force that acts on the electric field can be useful for countering problems caused by static electricity.
The table below shows the formulas based on Gauss’ theorem.
Based on Gauss’ theorem in the table below, the calculation of the electric field around a point or a line as different electric charge distribution indicates that the permittivity of the charged object is inversely proportionate to the electric field strength while the density of the lines of electric force is directly proportionate to the electric field strength. In other words, a sharp-tipped shape will have a large electric force density and consequently a stronger electric field.
| Shape of charge | Amount of electric charge | Electric field [V/m] | ||
|---|---|---|---|---|
| Point charge |
Q[C]
|
E = Q/4πε0r2
|
||
| Line charge |
λ [C/m]
|
E = λ/2πε0r
|
||
| Area charge |
δ [C/m2]
|
Electric field [V/m]
|
E = σ/ε0
|
Conductor
|
|
E = σ/2ε0
|
Insulator
|
|||
|
E = σ/ε0
|
Conductor
|
|||
|
E = σ/2ε0
|
Insulator
|
|||
| Cylinder |
ρ [C/m2]
|
Electric field [V/m]
|
E = ρr/2ε0
|
Inside cylinder
|
|
E = a2/2rε0
|
Outside cylinder
|
|||
|
E = ρr/2ε0
|
Inside cylinder
|
|||
|
E=a2/2rε0
|
Outside cylinder
|
|||
| Sphere |
ρ [C/m2]
|
Electric field [V/m]
|
E = ρr/3ε0
|
Inside sphere
|
|
E = ρa3/3ε0r2
|
Outside sphere
|
|||
|
E=ρr/3ε0
|
Inside sphere
|
|||
|
E = ρa3/3ε0r2
|
Outside sphere
|
|||
Distance from centre of charged object: r Radius of charged object: a Vacuum permittivity: ε0
Example:
In the case of an electric field with 1 [C] point charge
Distance from point charge to electric field is 1 [m]
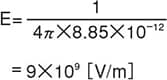
This is almost 1000 times the electrical breakdown strength in the air (3×106 [V/m]), comparable to a lightning discharge, and therefore is not practical.
For example, the amount of charge produced by rubbing a plastic surface with cloth is about 10-5 [C/m2] per unit area, so the electric field of the surface charge is as follows: